
AP Physics 1
Question 2 uses the term "overtone". "Overtone" is related to but not equivalent to "harmonic". An overtone is a harmonic above the fundamental frequency..
In a string tied at both ends, we know there are even and odd harmonics (1st, 2nd, 3rd, 4th, etc.) The first harmonic is also called the fundamental frequency (f1).
The second harmonic (f2), however, is also known as the first overtone in the string. That is, it is the first harmonic "over" the fundamental frequency.
The second overtone in the string would be the third harmonic, that is, the second harmonic over the fundamental frequency. And so on ....
In an air column with two open ends, there are also even and odd harmonics, just like the string tied at both ends. So the first overtone in an air column with two open ends is also the second harmonic (that is, the first harmonic "over" the fundamental frequency.
Things get a bit more confusing in an air column with one closed end. Here, there are no even harmonics, only odd (1st, 3rd, 5th, 7th, etc.). So the first harmonic "over" the fundamental frequency in an air column with one closed end is actually the third harmonic. The second harmonic "over" the fundamental frequency (that is, the second overtone) is the fifth harmonic. And so on ....
|
String tied at both ends or air column with two open ends |
First harmonic, also known as the fundamental frequency (f1) | Not applicable |
| Second harmonic (f2) | First overtone | |
| Third harmonic (f3) | Second overtone | |
| Fourth harmonic (f4) | Third overtone | |
| Air column with one closed end | First harmonic, also known as the fundamental frequency (f1) | Not applicable |
| There is no second harmonic | N/A | |
| Third harmonic (f3) | First overtone | |
| There is no fourth harmonic | N/A | |
| Fifth harmonic (f5) | Second overtone |
Keep the following in mind:
For a string fixed at both ends and for a pipe (air column) open at both ends, the wavelength of the fundamental frequency is 2 times the length of the string or pipe.

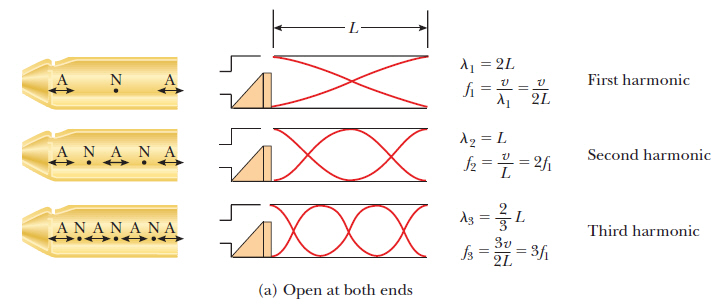
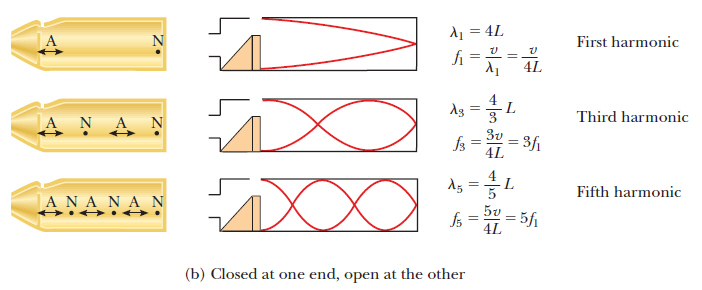
But, for an air column closed at one end, the wavelength of the fundamental frequency is 4 times the length of the pipe:
The relation between speed of sound in a medium and air temperature is given by the equation: v = (speed of sound in that medium at 273 K)(sqrt(T/273)), where T is the temperature of the air in Kelvin, and 273 is the Kelvin equivalent of 0 degrees C. We use Kelvin in physics as the standard unit of temperature.
That equation above can be used to find the speed of sound in helium based on the temperature of helium. (The actual equation for the speed of sound in a gas involves concepts that we do not study in this course. So the equation with the square root of T/273 is the best approximation.)
But, for sound in air, you can use an equation that approximates the formal equation above which uses temperature in C rather than K.
That equation is:
v = 331 + 0.6(Celsius temp). They will both give you the same approximate speed for air. But this second equation does not work for other media.
So for part b, you must use v = 965 m/s (sqrt(T/273)) to find the speed in helium.